The binary search is one of the first algorithms computer science students learn.
Below we're going to discuss how the binary search algorithm works and go into detail about how to implement the recursive binary search algorithm in Java — we'll provide an implementation for Python as well.
What is Binary Search?
Suppose you had a sorted array of elements.

Now suppose you needed to be able to find a particular element within that array.
One way to do it would be to go through each element one at a time starting from the beginning (or the end), this method is called linear search.
Linear search has a time complexity of O(n), which means the time it will take is proportional to the value of n.
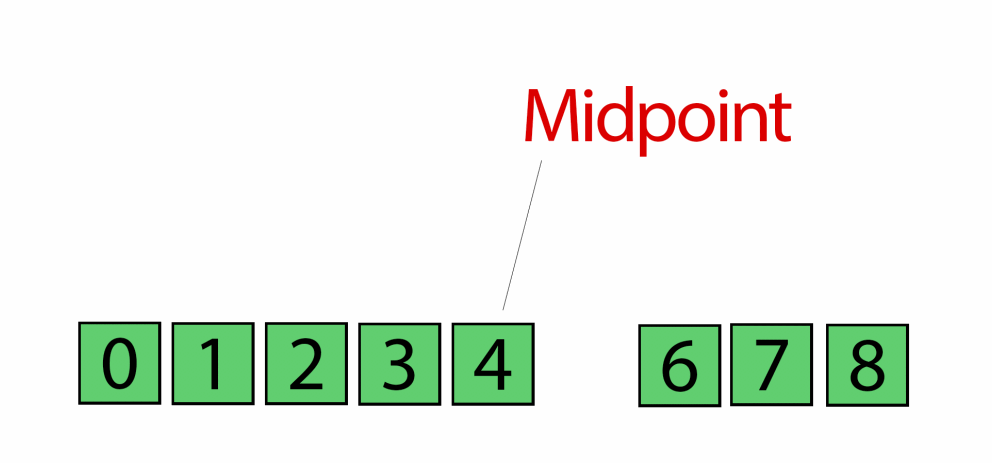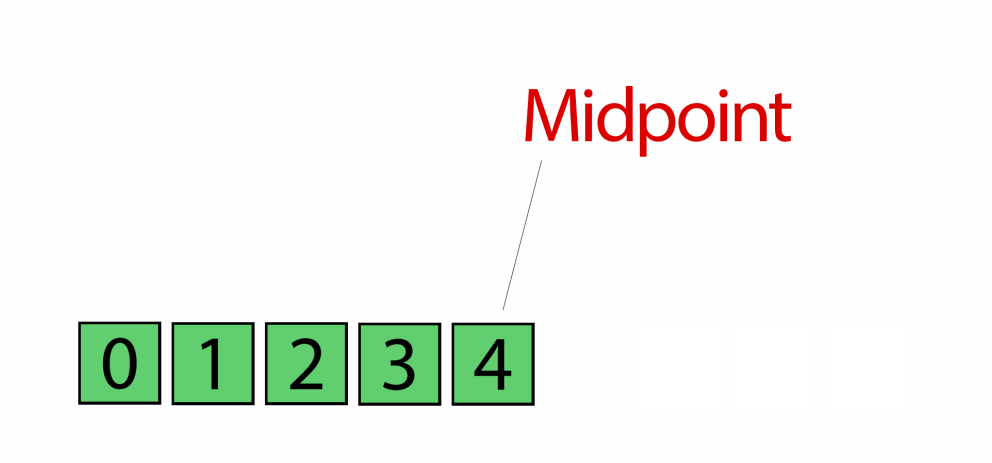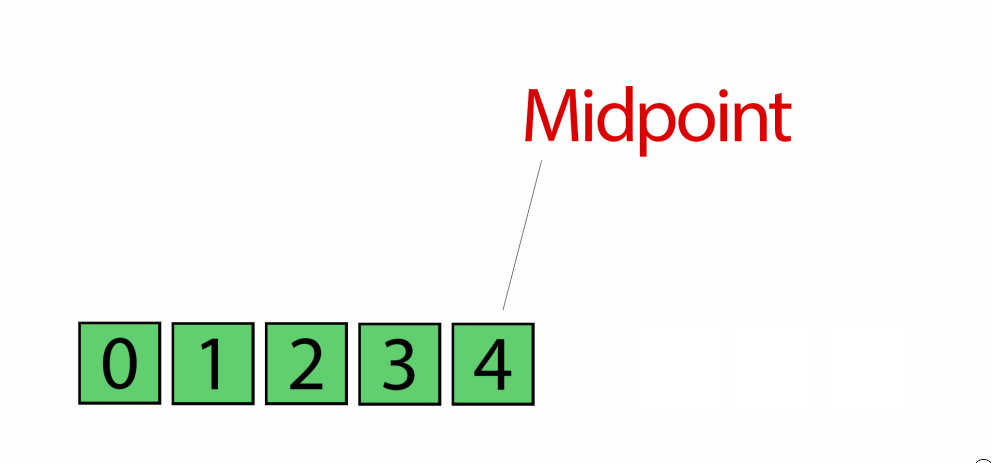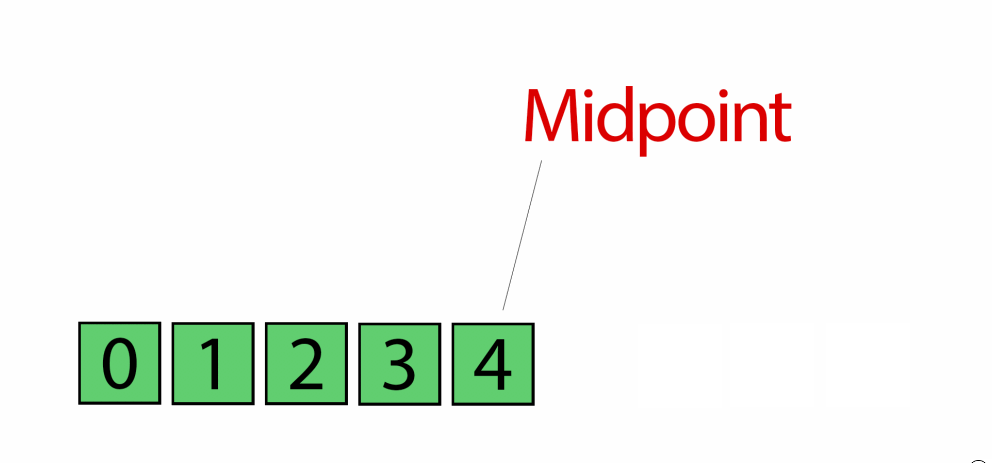
With binary search we select a value at the center of a sorted array, figure out if our value is greater or lower than our selected value, and then drop off whichever half our value isn't a part of.
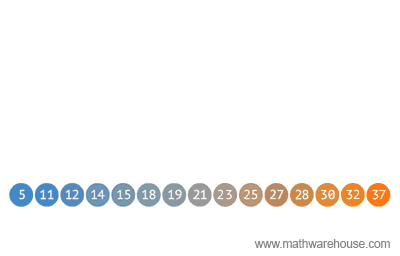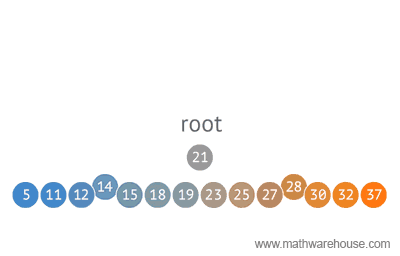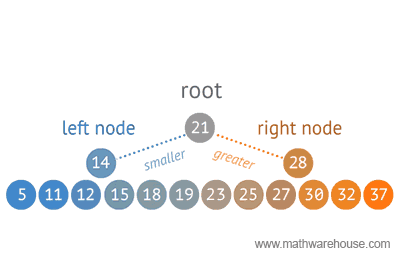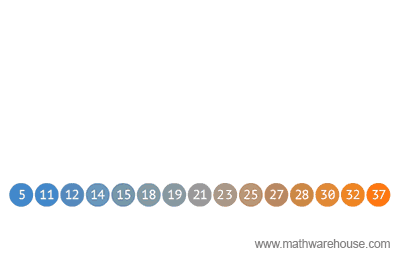
What is the Time Complexity of Binary Search?
Taking this approach we reduce the time complexity to O(Log n).
Recursive Implementation of Binary Search in Java
Declare a Class
We'll start by declaring a class and giving it a name of BinarySearch.
Create the Method
Next we'll create our method (we'll name it binarySearchMethod) which takes four arguments:
- A sorted array
- 3 integer variables
leftTail represents the value at index 0 of our array. This should be the smallest value in the array.
rightTail should be the last value in the array (array.length - 1).
selectedValue is the value we're actually looking for.
Body of the Method
Within our body we'll start with our outer conditional, which checks whether or not the rightTail is ≥ leftTail.
If it is, then we create a middle value (e.g., midValue) that will be equal to half the value of the leftTail plus the value of our rightTail – 1.
Okay, that may be a bit confusing so let's write it out:
Within our conditional we have more conditions though!
We'll check to see if our midValue is equal to our selectedValue and if it is, great, we can stop checking because we've found our answer (e.g., return midValue).
Time for Recursion
Otherwise, we'll check and see if our midValue is greater than our selectedValue.
If midValue is greater than selectedValue then we know that our value is somewhere between our leftTail and our midValue, right?
So we can now drop off all of the values greater than our midValue.
This is where our first bit of recursion occurs.
To do this we'll call our binarySearchMethod again and pass to it our sortedArray, our leftTail, our midValue – 1, and our selectedValue.
Déjà Vu
We wrap our up our outer conditional by recursively calling the binarySearchMethod again.
You see, if our midValue wasn't equal to our selectedValue nor greater than our selectedValue, then it must be less than our selectedValue.
In which case we drop all values to the left our of midValue and begin again.
So we'll call our binarySearchMethod and pass to it our sortedArray, our leftTail becomes midValue – 1, our rightTail, and finally our selectedValue.
Wrapping Up our binarySearchMethod
Now we wrap up our binarySearchMethod by terminating it. To do this we can return – 1.
If we don't…well, we'll get a compilation error due to a missing return statement.
Let's Test Our Method
Unit Testing
We can test our method in a variety of ways. We'll test it using unit tests.
We'll cover how to create unit tests in a later post, but for now, see below.
Test Using System.out.println
You can also run some tests by calling the method and returning output to the print line. See below for the full implementation.
Complete Recursive Binary Search Algorithm in Java
Recursive Binary Search in Python
Keep Learning
I hope this resource helped you understand the Binary Search algorithm. If you have any questions or suggestions, feel free to drop us an email. We would be glad to receive the input.
If you're feeling up to it, you can learn a bit more about the binary search algorithm by visiting the very well written Wikipedia page article on it.
